曲线，一个更接近完美的答案

编注：视频文字稿内容由少数派整理以方便阅读查找，要了解完整信息，建议直接观看视频。

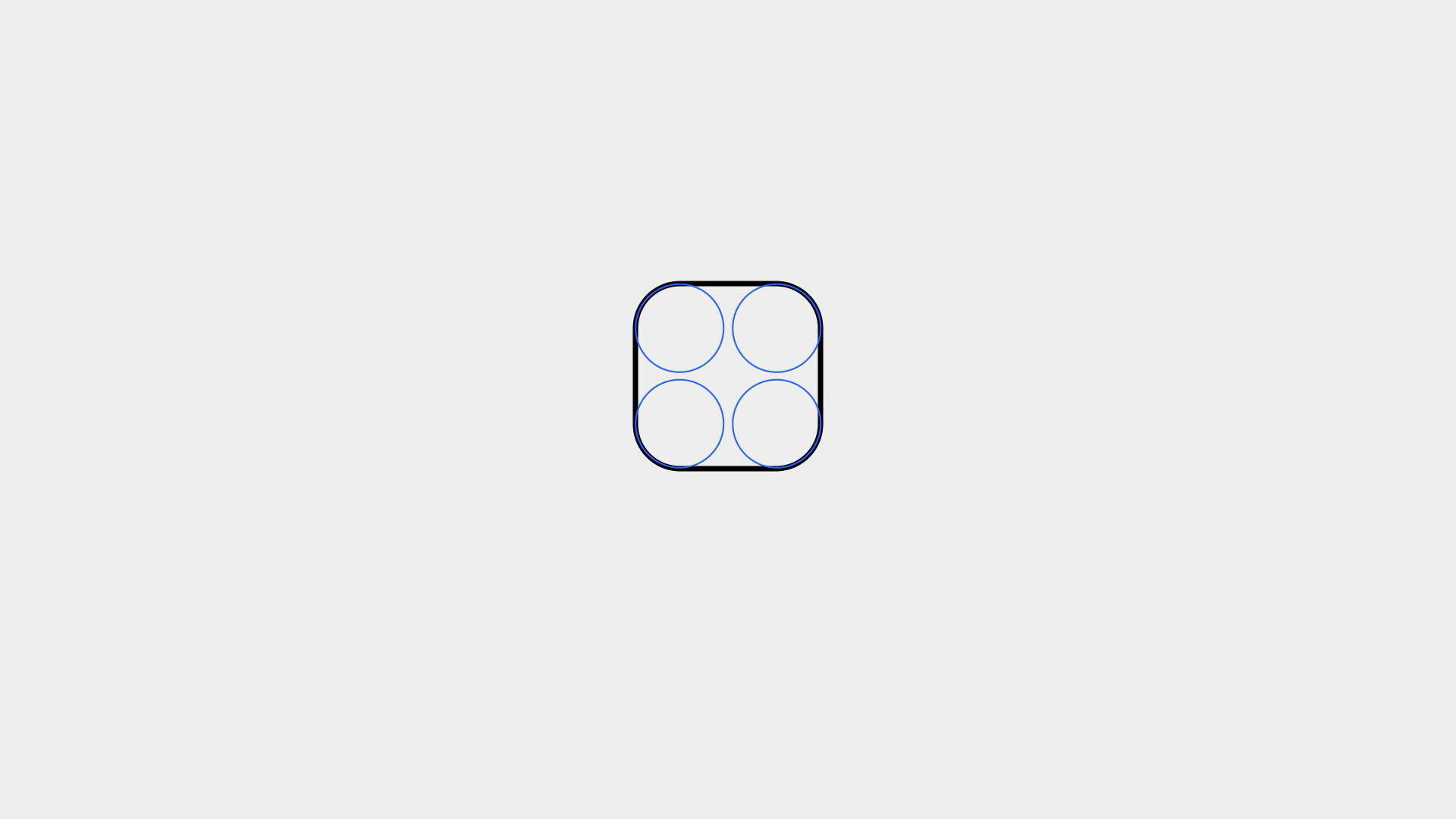
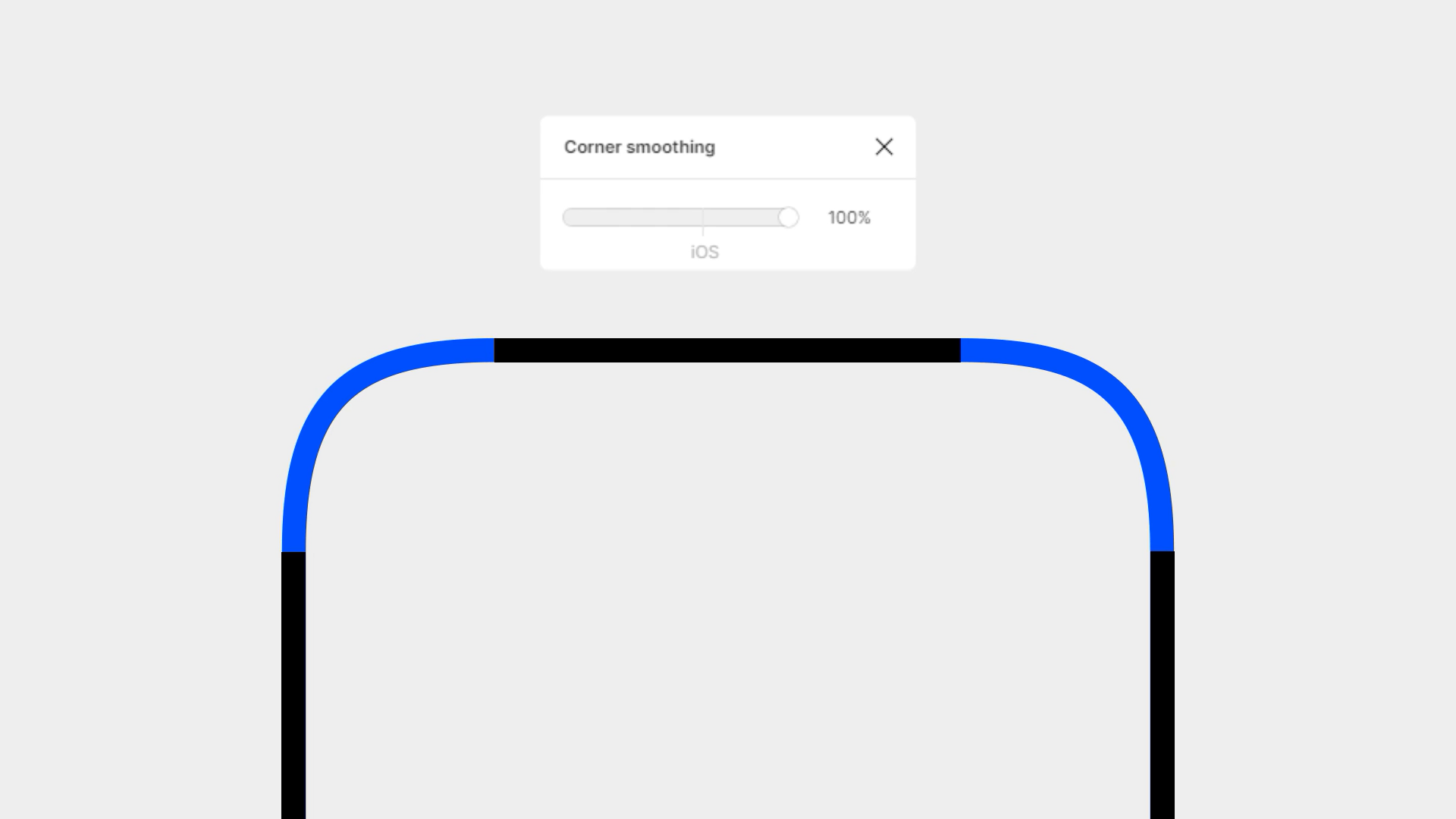
这是一个完美的正方形，每条边都十分平滑、顺畅，没有瑕疵。试着把尖角变成 1/4 的圆进行连接，便得到了一个圆角矩形。在大多数平面绘图软件中，圆角矩形都是用这种方法绘制出来的。但是它的线条足够顺滑吗？

我们放大它的一角，在曲线与直线连接的地方过渡其实是不自然的。200多年前，人们便开始尝试对平滑过渡的曲线进行计算，于是后来便诞生了很多种缓和曲线，在诸如测绘、工业设计之类的工作中起着十分重要的作用。

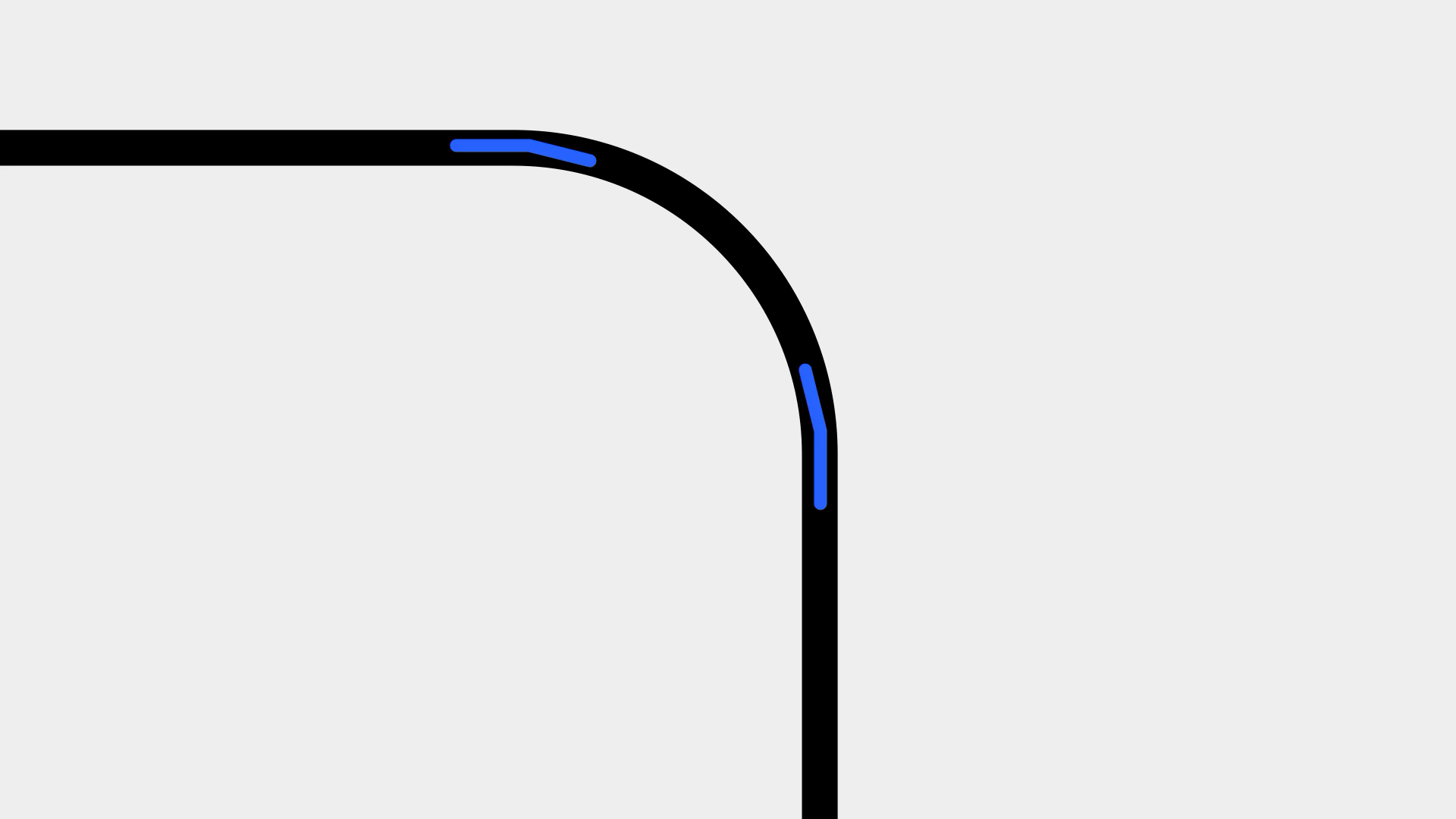
画面中的「羊角螺线」就是其中之一，我们使用羊角螺线起点处的这段曲线绘制一个圆角矩形，会得到一个过渡十分顺滑的结果。相比之下，右边那个简单粗暴的圆角矩形，也就显得十分粗糙。

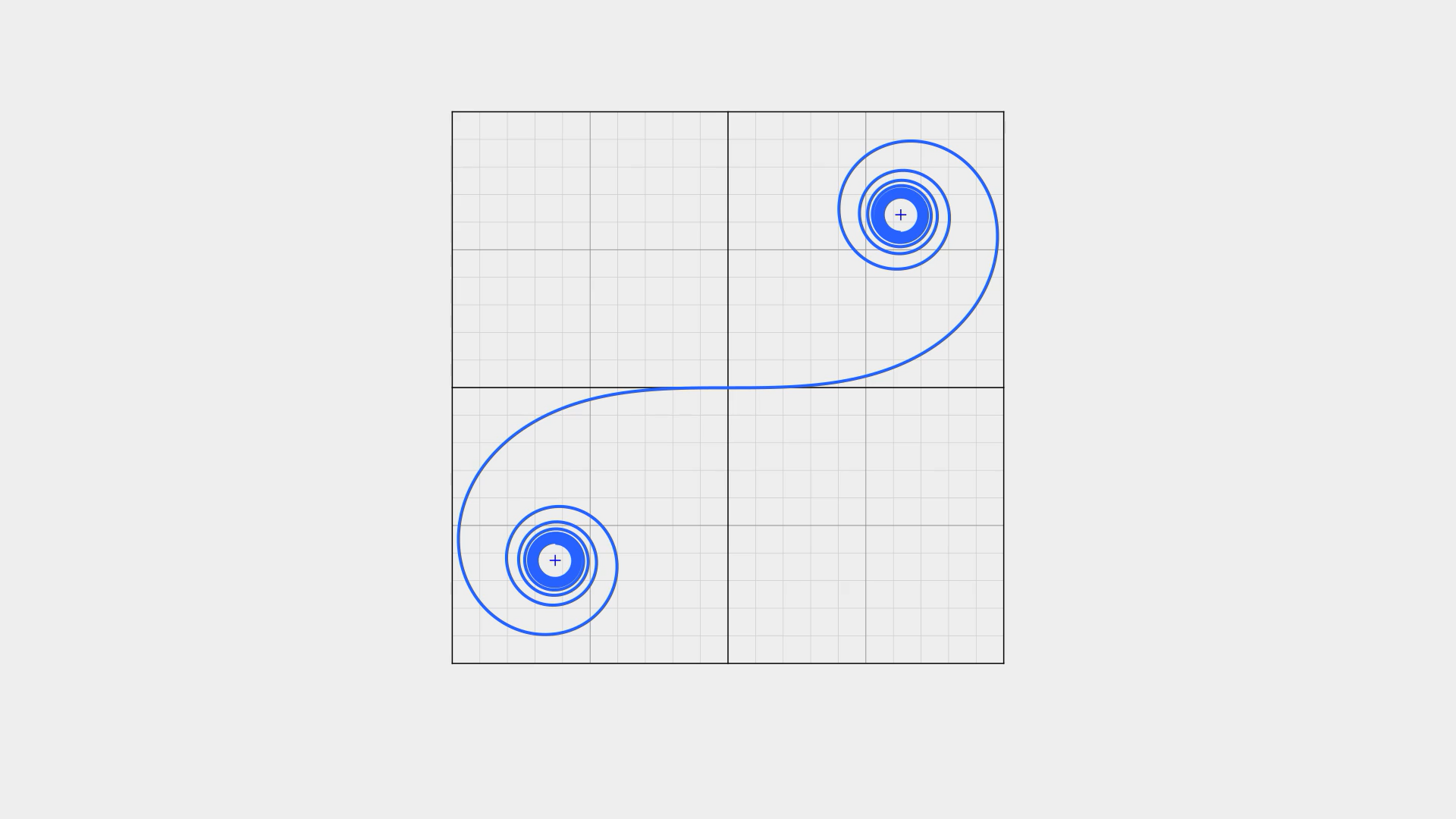
而经过优化的形状，与 中 App 图标的轮廓看起来几乎一模一样。在 iOS 7 之后，苹果开始大规模采用这种曲线过渡的规范，使得「曲率连续」这个概念不再由专业设计师独享，而是成为了更多爱好者们所热衷的话题，「G2 连续」这个词也被更多人所熟知。

仅仅是点与点的贴合可以称为「G0 连续」，在点与点连续的基础上如果还有相切关系，那就可以称为「G1 连续」，而如果它们的曲率还有着更为连续的变化，可以称为「G2 连续」。当然，这种描述并不精确，但是理解至此暂且足够。

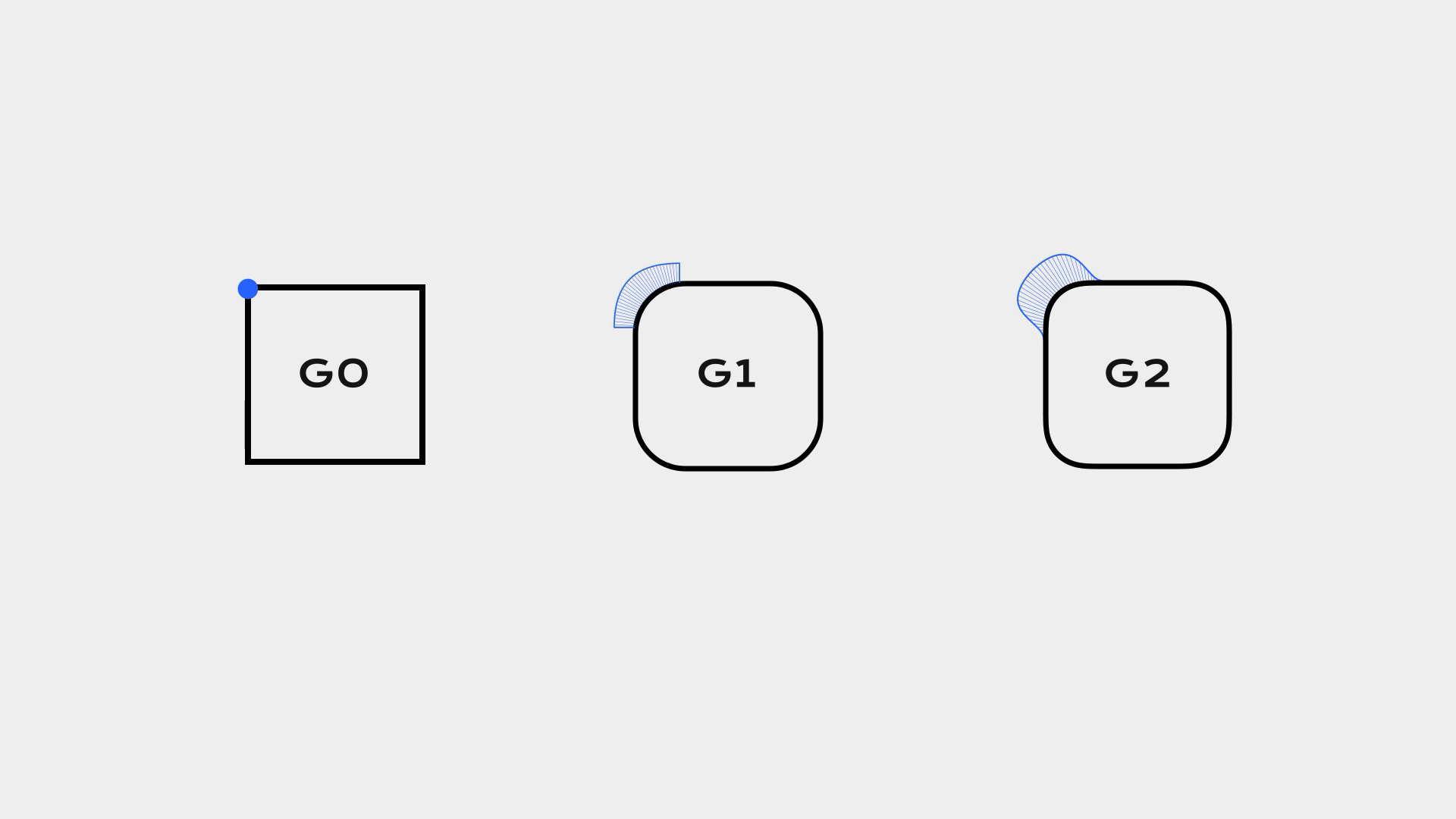
用通俗点的方法来说，其实就是让曲率以一种看起来好像先慢后快的方式达到峰值，使其更加顺滑，这与动画中的速度曲线倒还有那么一点点的异曲同工之妙。如果以匀速前进，看起来就会比较生硬，而如果让它突然加速再缓慢停止，就会模拟惯性，产生一种丝滑的感觉。

在很多平面软件中绘制曲线的功能被称为「钢笔工具」，而它们的本质一般都是一种叫做的「贝济埃」的曲线，其实更多时候人们愿意称其为「贝塞尔」。这次所聊的 Bézier 曲线由法国人提出，所以按照法语发音应该叫做「贝济埃」更为恰当。

这是一种通过设定几个点然后插值进行拟合的方法，数理逻辑在这里不做深究。我写了一个模拟程序进行演示，看看就好。

通过递归的方式，我们可以绘制出更高阶的贝济埃曲线。以 、 为首的平面软件产品，采用的都是三次贝济埃曲线。但 的曲率工具和 的钢笔智能模式分别使用了完全不同的算法，这两种算法产生的曲线必然经过节点，无法通过手柄进行灵活的调整，但是却能够自动生成较为顺滑的曲线，在 CAD 中这比较常见，这里就不多赘述了。

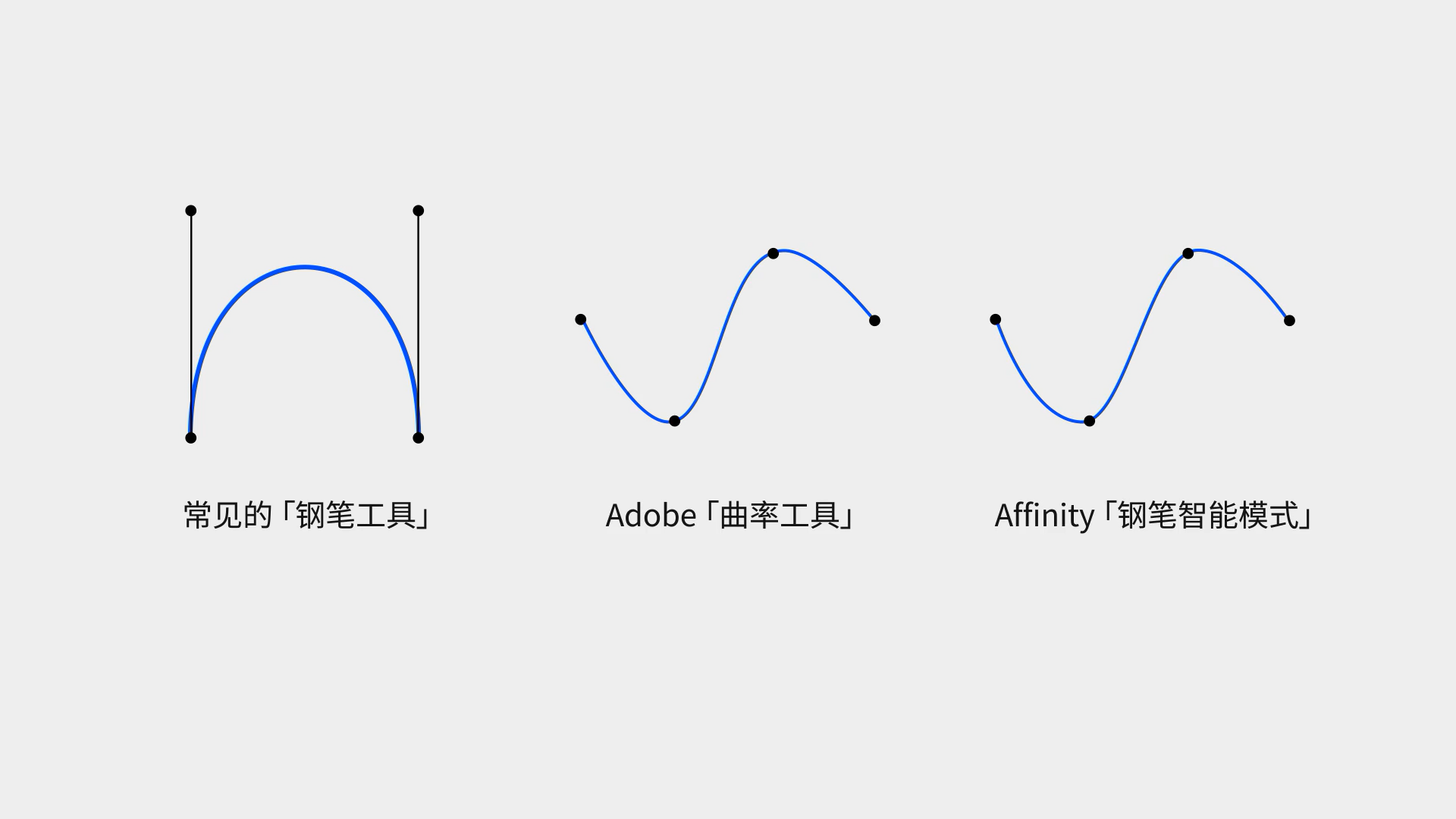
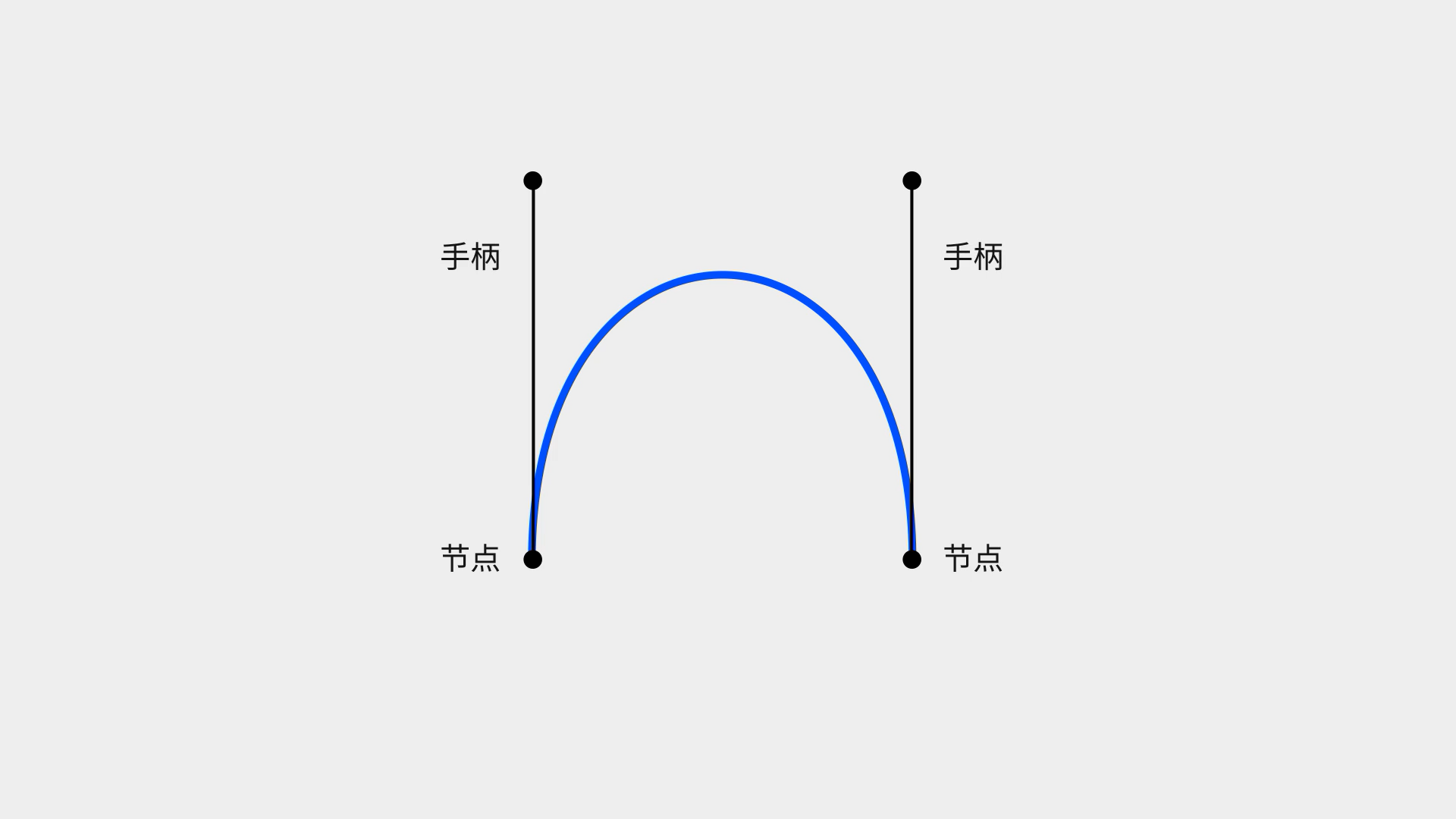
去掉三次贝济埃曲线内部的杠杆，便是我们所熟知的钢笔工具的模样了。起始点与结束点就是我们在软件中绘制的节点，而其余两个点形成了我们用来调整曲线的手柄。设计师们如何才能在节点繁多、复杂的情况下，绘制出连接更顺滑的曲线呢？

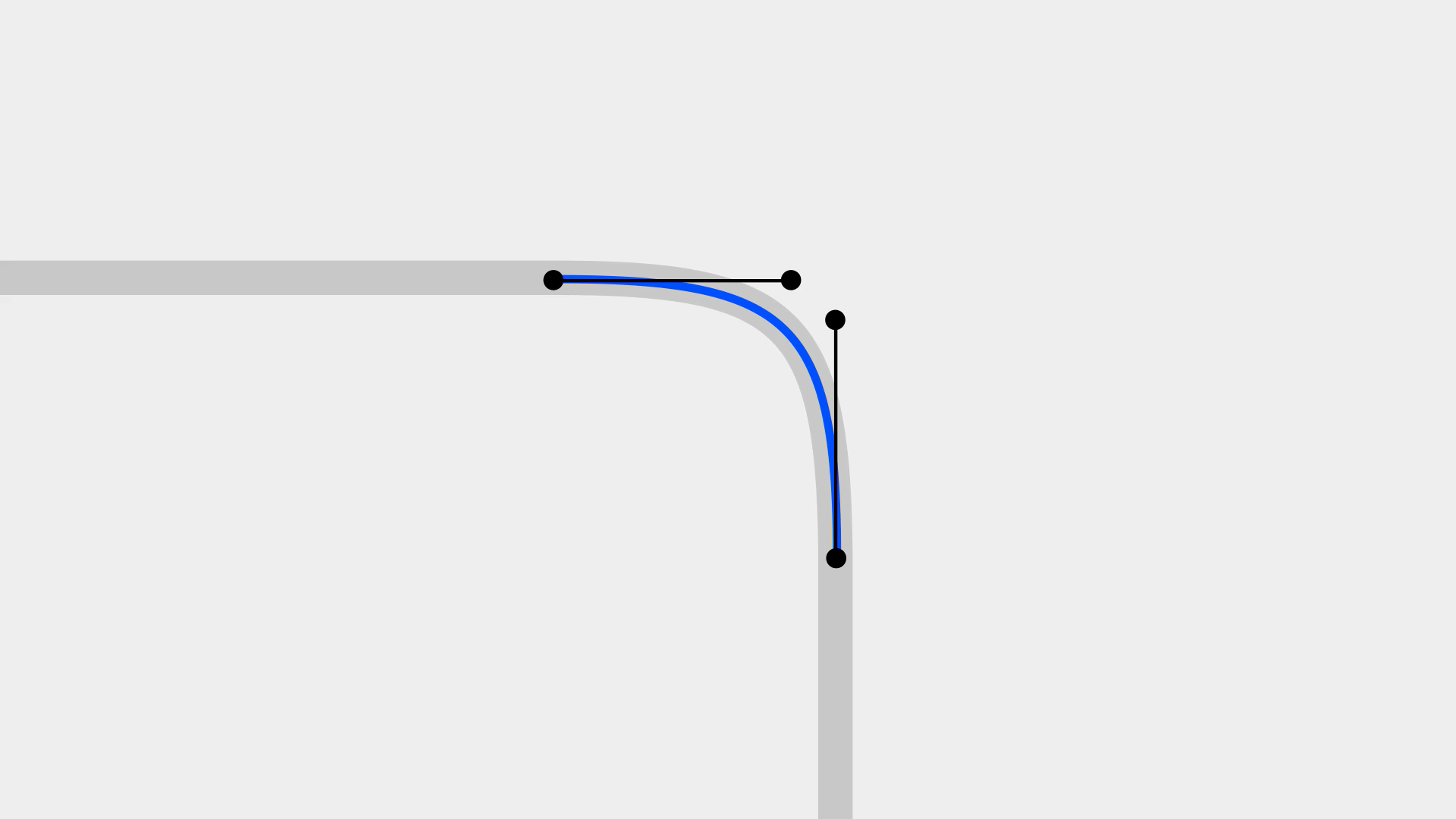
回到短片开头，那个粗糙的圆角矩形，我们将每一个节点向内进行偏移，然后再适当拉长手柄，其实就可以对曲率连续进行一定程度的优化。这种调整在数理上并不精准，但在平常的工作中如果只是为了满足观众的视觉其实已经足够了。

有一些软件中有着相关功能，比如 中的 原生就能满足这个需求。

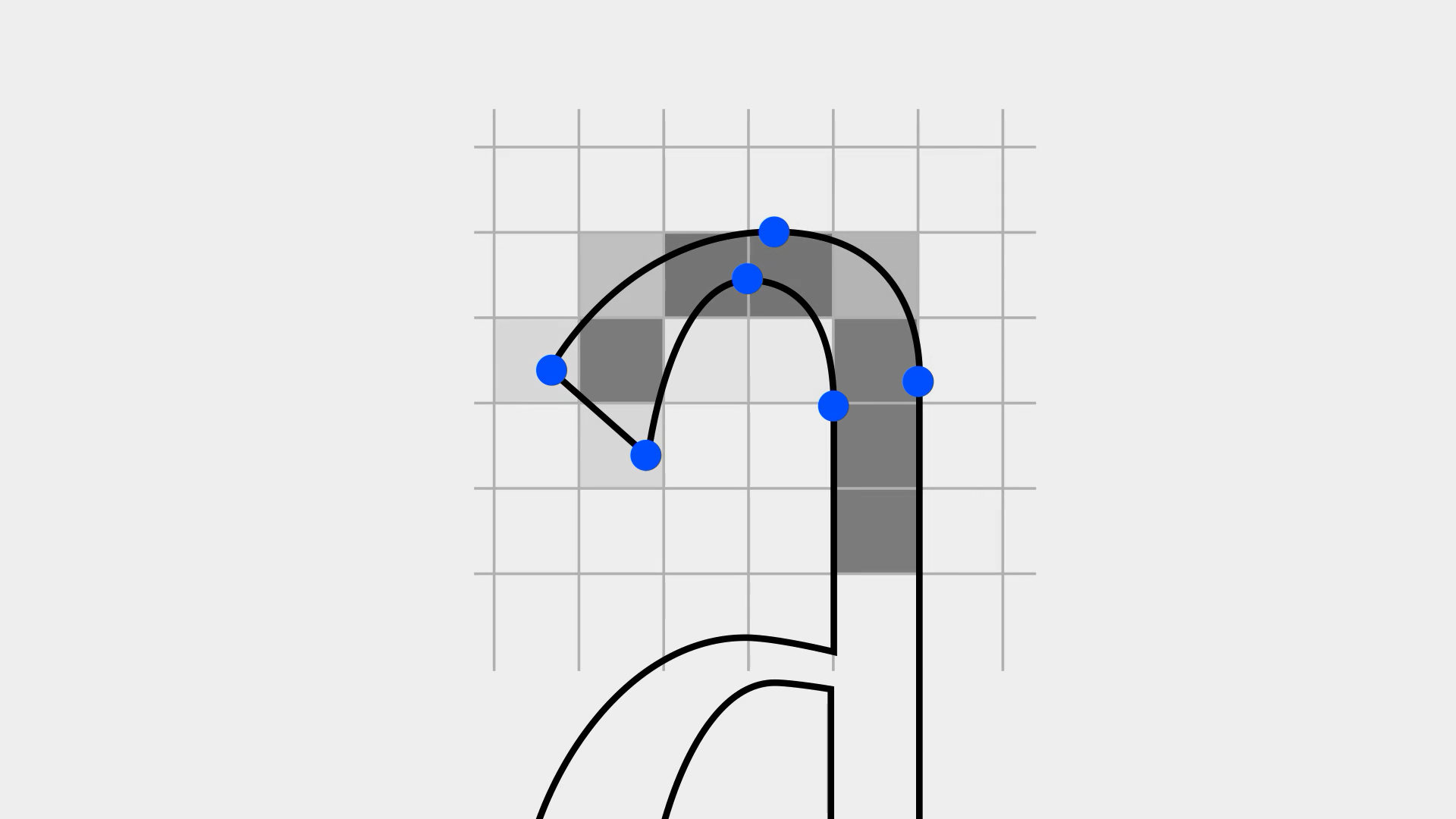
在使用贝济埃曲线进行绘制的时候，有着一个重要的规范。首先要尽可能的将节点放在「极值点」的位置，然后让节点与手柄保持水平或垂直对齐，这可以让绘制变得更加容易。因为这样只需要调整手柄的长度就可以拟合自己想要的曲线结果，这个规则在字体设计中尤为重要。

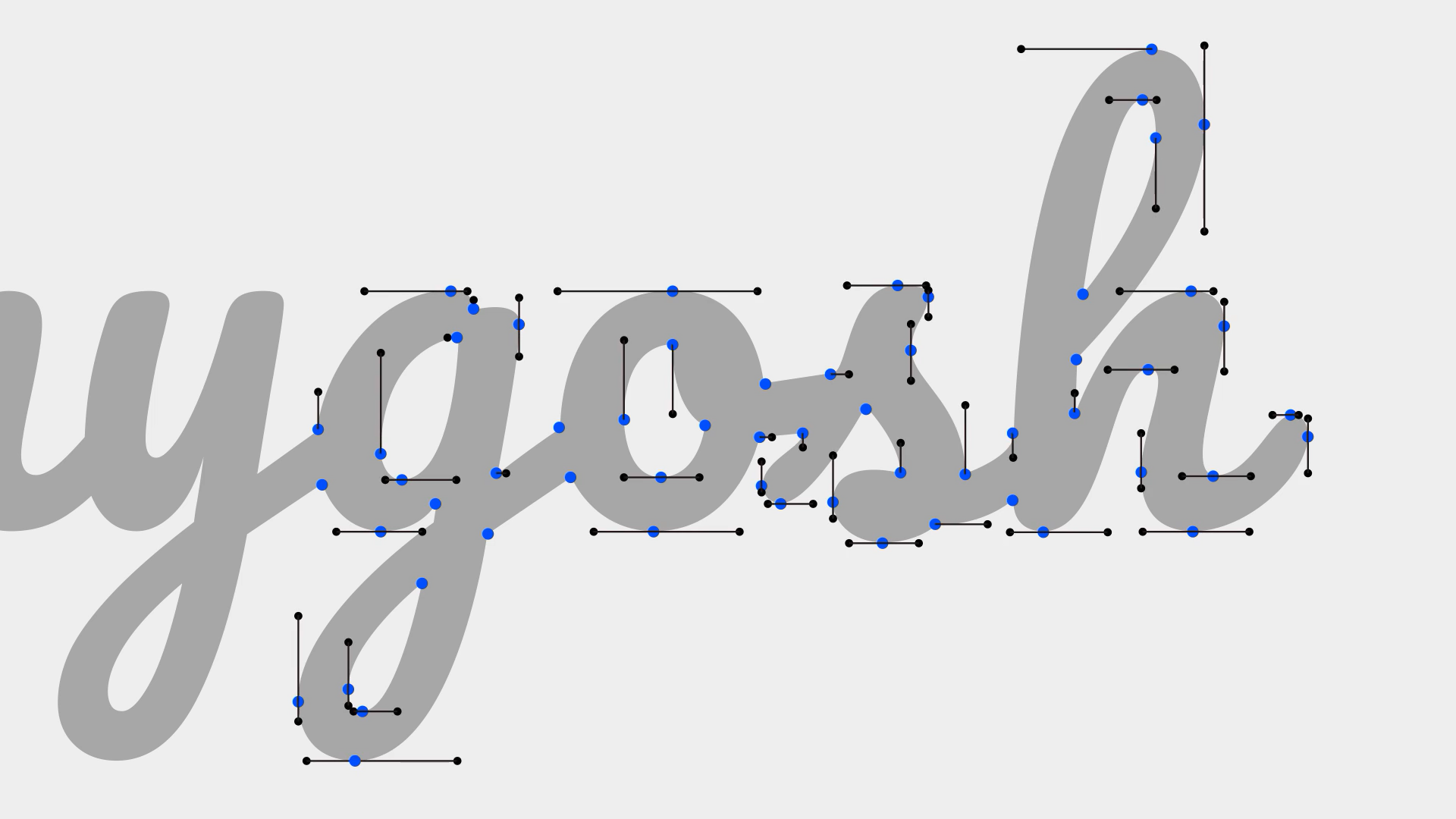
因为在低精度屏幕上，算法会根据这种位置的节点对显示效果加以优化，专业的字体设计软件甚至会有自动添加极值点的功能，但是在例如宣传美术、艺术插画领域等，这些最终会输出固定精度位图的情况，倒也可以适当放松标准。

在字体设计领域中也有着经典的案例，「筑紫明朝体」是一款应用于印刷及平面设计领域的字体，并不是为了在数位屏幕上显示而设计的。藤田重信用极少的节点数量绘制了优美的曲线线条，相应地也就降低了字体文件的大小，品质极高。

了解了这些规范，我们尝试着绘制这样的一个形状。你可能会在起始、结束、中间设定三个节点构成这个形状，但这样我们会发现线条中间出现了不顺畅的情况，还需要对这个节点进行单独的调节。而调整后，他与手柄也无法以水平的对齐方式存在了。

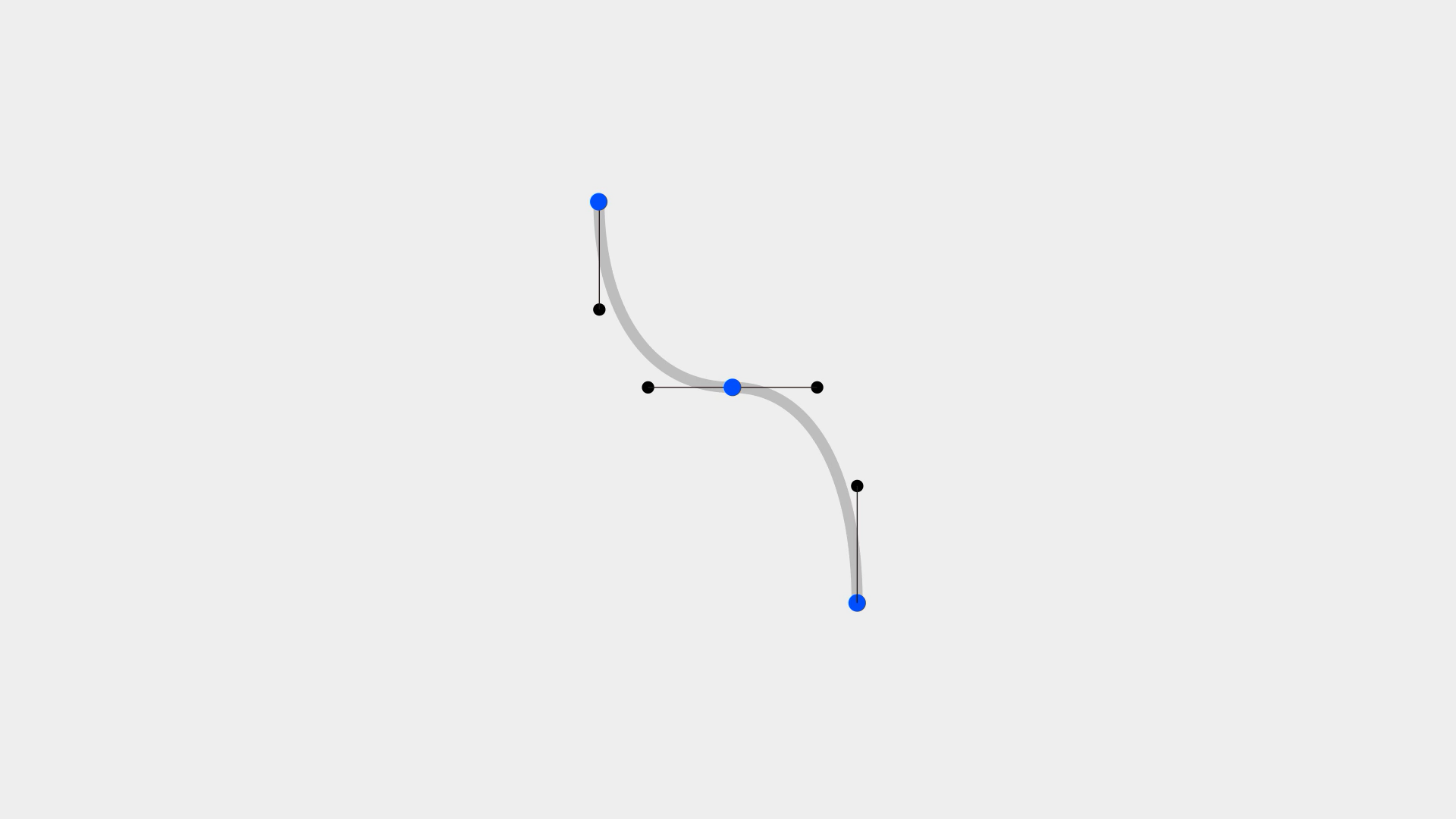
但其实我们将这个节点删除，拉长两端的手柄，同样可以绘制出这个形状。如此看来，之前中间的点就是在徒增烦恼。这个案例告诉我们，要在满足效果的前提下，尽可能简化节点的数量。即便如此，一个图形还是有可能以多种不同的布点方式绘制出来，都是熟能生巧和经验之谈了，需要我们勤加练习。

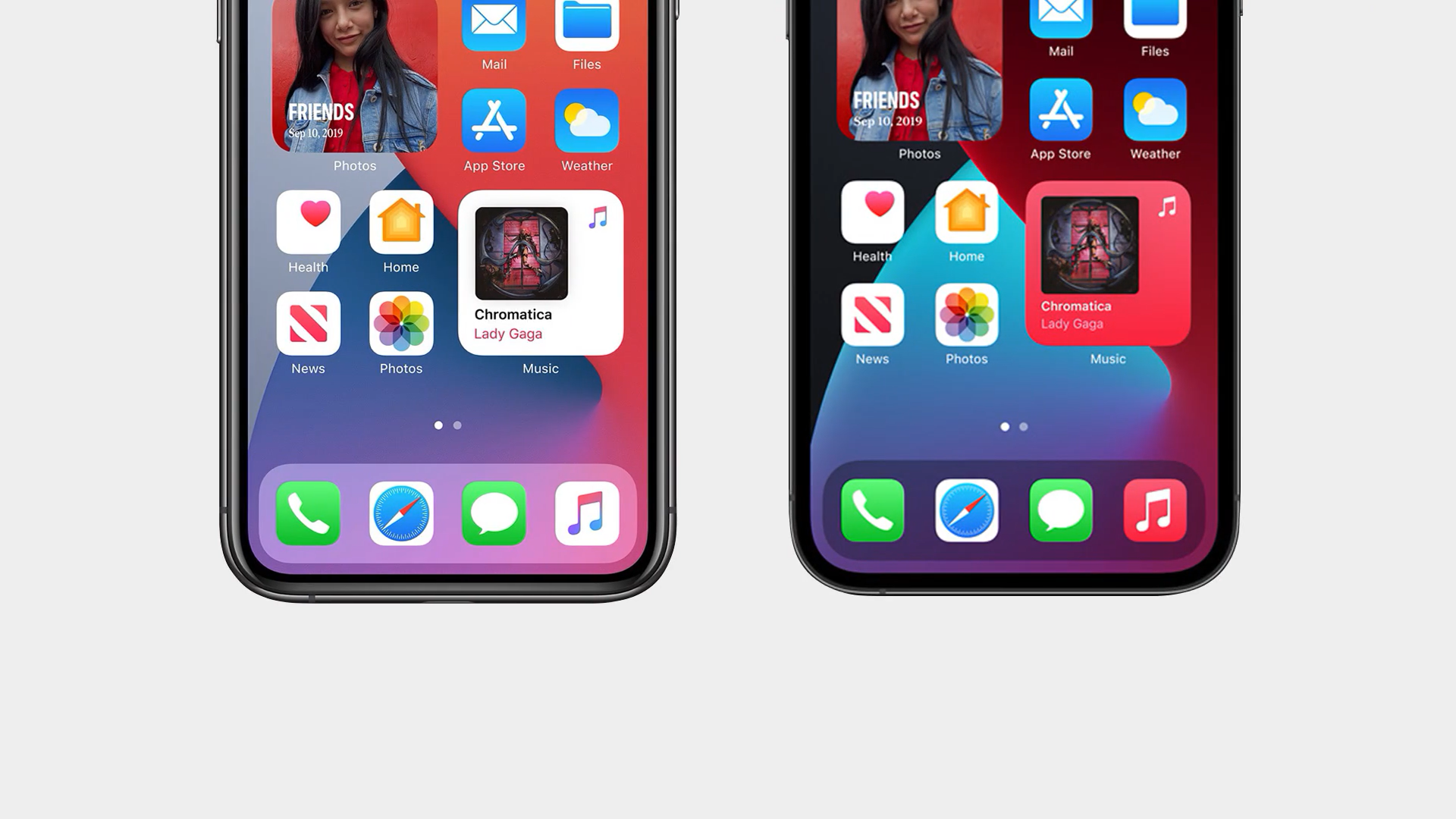
这是 X 底部的 Dock 栏，而这是 12 底部的 Dock 栏。相同的系统，却有着完全不同曲率的圆角。这是为了和机身外观的圆角形成更好的呼应。曲率从工业设计走进图形领域，从平面之外传播到平面之内，这一条条排比舒适的顺滑曲线却又让它在平面之内超越了平面。

我们在设计的究竟是什么，是圆角吗？不。

是在设计一个更接近完美的答案。